We use MathJax

A Gallery of Conic Sections

The equation of each conic section is a second-degree polynomial function of two variables, and can be written in the form   $a_1x^2+a_2xy+a_3y^2+a_4x+a_5y+a_6=0$.   One property common to each of these curves is that it will intersect any given line at most 2 times. Non-degenerate quadratic plane curves are often called conic sections, since each can be obtained by slicing a double-napped cone.

Each of the graphs on this page is a quadratic plane curve, displayed in the window   $[-5,5]\times[-5,5]$.

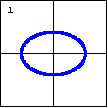
	$4x^2+9y^2-36=0$ An ellipse is one type of quadratic plane curve, or conic section.
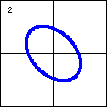	$13x^2+10xy+13y^2-72=0$ Ellipses can be oriented in any direction. They do not have to be symmetric with either axis.
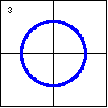	$x^2+y^2-9=0$ A circle is also a quadratic plane curve, or conic section. A circle can also be viewed as a very special ellipse.
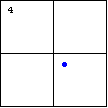	$x^2+y^2-2x+2y+2=0$ When the radius of a circle shrinks to zero, a degenerate circle will result. In other words, a single point is one type of quadratic plane curve. Interestingly, this graph can also be described as the union of two intersecting lines having slopes $\pm i$, each passing through the point   $(1,-1)$.
	$x^2+y^2+9=0$ Quadratic equations in two variables may have no real solutions. Examining the equation, you might be inclined to describe this as a circle with an imaginary radius.
	$x^2-y^2-4=0$ A hyperbola is also a quadratic plane curve, or conic section.
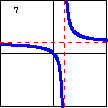	$xy-x-y=0$ Hyperbolas can be functions, if one of the asymptotes is vertical.
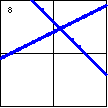	$x^2-xy-2y^2+x+10y-12=0$ Here is a degenerate hyperbola, which will result when the constant term of a hyperbola is changed to zero.
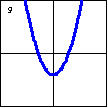	$x^2-y-2=0$ A parabola is also a quadratic plane curve, or conic section.
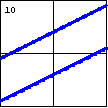	$x^2-4xy+4y^2-16=0$ Quadratic equations in two variables can also produce the degenerate case of two parallel lines.
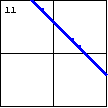	$x^2+2xy+y^2-6x-6y+9=0$ Another degenerate case of a quadratic equation will produce a single line, though with multiplicity two. This occurs when the equation is a perfect square on one side, and zero on the other.